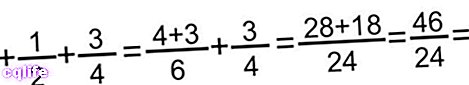אנו מסבירים מהי חיבור או חיבור במתמטיקה, ההיסטוריה שלה, תכונותיה ודוגמאותיה. כמו כן, שיטות להוספת שברים.

מה הסכום?
התוספת או התוספת היא פעולה מתמטית בסיסית, המורכבת משילוב של אלמנטים חדשים ל-a מַעֲרֶכֶת מספרי, כלומר לאיחוי של שני מספרים כדי לקבל אחד חדש, המבטא את הערך הכולל של השניים הקודמים. התוספת היא העיקרון הבסיסי איתו אנו לומדים להתחבר למספרים, שכן עצם הספירה אחד אחד (1, 2, 3, 4...) כרוכה בהוספת 1 (1 + 0, 1 + 1, 1 + 2, 1 + 3...).
הסכום הוא פעולה מסוג אריתמטי, המאפשרת שילוב של מספרים מסוגים שונים: טִבעִי, מספרים שלמים, שברים, ממשיים, רציונליים, לא רציונליים ומורכבים, וכן מבנים הקשורים אליהם, כגון מרחבים וקטוריים או מטריצות. בְּ אַלגֶבּרָה המודרניזם מיוצג על ידי הסמל +, המוכנס בין האלמנטים שיתווספו, ומתבטא מילולית כ"עוד": "1 + 1 = 2" נקרא "אחד ועוד אחד שווה שניים".
מצד שני, האלמנטים שיש להוסיף ידועים כ"מוסיף", והמספר המתקבל בסוף נקרא "תוצאה".
היסטוריה של הסכום
הוספה היא אחת הפעולות המתמטיות העתיקות והבסיסיות ביותר הידועות. נהוג לחשוב כי ה בן אדם מהתקופה הניאוליתית היא כבר טיפלה בעקרונות מתמטיים אלמנטריים, שביניהם יהיו בהכרח חיבור וחיסור, שכן פעולות אלו קלות להוכחה לנוכח האספקה החקלאית שגדלה וירדה בהתאם לתקופת השנה.
עם זאת, חקר החיבור ויישומה הן למספרים הטבעיים והן למספרים השברים החל במצרים הקדמונים, והמשיך להתפתח בדרכים מורכבות יותר עם הבבלים, ובעיקר עם הסינים וההינדים, שהיו הראשונים שהוסיפו מספרים. . אבל רק ב רֵנֵסַנס הפריחה הבנקאית כפתה את סכום העשרונים והלוגריתמים הוולגריים.
מאפייני הסכום
לתוספת כפעולה מתמטית יש קבוצה של מאפיינים, שהם:
- נכס קומוטטיבי. הוא קובע שסדר התוספות אינו משנה את התוצאה, כלומר ש-a+b זהה לחלוטין ל-b+a, ובשני המקרים מתקבלת אותה תוצאה.
- רכוש אסוציאטיבי. הוא קובע שכאשר מוסיפים שלושה אלמנטים או יותר, ניתן לקבץ שניים מהם כדי לפתור אותם תחילה, ללא קשר למה שהם, מבלי לשנות את התוצאה הסופית. כלומר, אם נרצה להוסיף a + b + c, נוכל לבחור בשתי דרכים: (a + b) + c או a + (b + c), מבלי להשפיע כלל על התוצאה.
- נכס זהות. הוא קובע שאפס הוא אלמנט נייטרלי בפעולה, כך שהוספתו עם כל מספר אחר תביא תמיד לאותו מספר אחרון: a + 0 = a.
- סגירת נכס. היא קובעת שתוצאת סכום תהיה שייכת תמיד לאותה קבוצה מספרית של תוספות, כל עוד אלה בתורם חולקים את אותה קבוצה. כלומר, אם התוספות a ו-b שייכות ל-N (טבעי), Z (מספרים שלמים), Q (אי-רציונלי), R (ממשי) או C (מורכב), גם תוצאת הסכום תהיה שייכת לאותה קבוצה.
דוגמאות לתוספת
הנה כמה דוגמאות פשוטות להוספה:
- לאישה יש ארבעה פרחים, אבל זה יום ההולדת שלה וניתנים לה עוד שמונה. כמה פרחים יש לו בסוף היום? 4 פרחים + 8 פרחים = 12 פרחים.
- לרועה יש 15 כבשים, ולעמית שלו יש 13. אם הם יחליטו למזג את העדרים שלהם, כמה כבשים יהיו להם בסך הכל? 15 כבשים + 13 כבשים = 28 כבשים.
- עץ תפוח נותן לבעליו 5 תפוחים בחודש. כמה תפוחים יהיו לו בתום שנה אחת? מכיוון ששנה היא 12 חודשים, עלינו להוסיף 5 שתים עשרה פעמים, תוך יישום המאפיין האסוציאטיבי: (5 + 5) + (5 + 5) + (5 + 5) + (5 + 5) + (5 + 5) + ( 5 + 5) = (10 + 10) + (10 + 10) + (10 + 10) = 20 + 20 + 20 = 60 תפוחים בשנה.
סכום השברים
כאשר מוסיפים שברים, ישנם שונים שיטות שנוכל ליישם כדי להשיג את התוצאה, תלוי אם מדובר בשברים תקינים, לא תקינים ומעורבבים.
- שיטה לחיבור שברים עם אותו מכנה. זהו המקרה הפשוט ביותר, בו אנו פשוט מוסיפים את המונים ונשמור על אותו מכנה. לדוגמה:
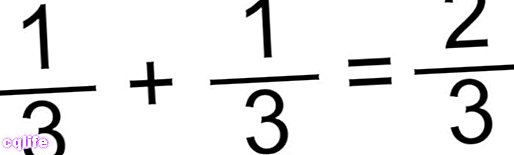
אוֹ
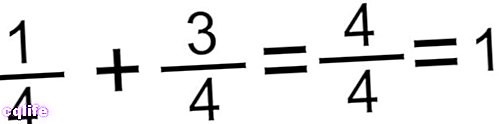
- שיטת פרפר. שיטה זו מאפשרת לנו להוסיף כל סוג של שברים עם מכנים שונים, פשוט להכפיל את המונה של הראשון במכנה של השני ולהיפך, ולאחר מכן להוסיף את התוצרים (כדי לקבל את המונה), ולאחר מכן להכפיל את המכנים כדי לקבל המכנה של השבר הסופי. לאחר ביצוע פעולות אלו, לעיתים קרובות נצטרך לצמצם את התוצאה. לדוגמה:
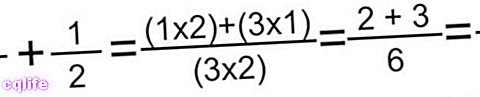
- שיטה להוספת שלושה שברים. במקרה זה, אנו פשוט מוסיפים את השניים הראשונים ומוסיפים את האחרון לתוצאה, מיישמים את השיטה הקודמת ומצמצמים או מפשטים את התוצאה במידת הצורך. לדוגמה: