אנו מסבירים הכל על המשולש, תכונותיו, היסודות והסיווג שלו. כמו כן, כיצד מחושבים השטח וההיקף שלו.

מהו משולש?
המשולשים או הטרינים הם דמויות גיאומטריות שטוחים, בסיסיים, שיש להם שלושה צדדים במגע זה עם זה בנקודות משותפות הנקראות קודקודים. שמו בא מהעובדה שיש לו שלוש זוויות פנימיות או פנימיות, שנוצרות על ידי כל זוג קווים במגע באותו קודקוד.
דמויות גיאומטריות אלו נקראות ומסווגות לפי צורת הצדדים שלהן וסוג הזווית שהן עושות. עם זאת, הצלעות שלו תמיד שלוש וסכום כל הזוויות שלו תמיד ייתן 180 מעלות.
משולשים נחקרו על ידי ה אֶנוֹשִׁיוּת מאז ומתמיד, מאז הם היו קשורים לאלוהי, עם מסתורין וקסם. לכן, אפשר למצוא אותם בסמלים נסתר רבים (בַּנָאוּת, כישוף, קבלה וכו') ובמסורות דָתִי. המספר המזוהה שלו, שלוש, רומז נומרולוגית לתעלומת ההתעברות והחיים עצמם.
בהיסטוריה של המשולש ה העת העתיקה היוונית מגיע למקום נכבד. פיתגורס היווני (בסביבות 569 - 475 לפנה"ס לערך) הציע את המשפט המפורסם שלו למשולשים ישרים, הקובע שריבוע התחתון שווה לסכום ריבוע הרגליים.
מאפייני משולש
התכונה הברורה ביותר של משולשים היא שלוש הצלעות שלהם, שלושה קודקודים ושלוש זוויות, שיכולות בהחלט להיות דומות או שונות לחלוטין זו מזו. משולשים הם המצולעים הכי פשוטים שיש וחסר להם אלכסון, שכן בכל שלוש נקודות לא מיושרות אפשר ליצור משולש.
למעשה, ניתן לחלק כל מצולע אחר לקבוצה מסודרת של משולשים, במה שמכונה שִׁיטַת מְשׁוּלָשׁ, אז חקר המשולשים הוא יסוד לגיאומטריה.
כמו כן, משולשים הם תמיד קמורים, לעולם לא קעורים, מכיוון שהזוויות שלהם לעולם לא יכולות לעלות על 180 מעלות (או π רדיאנים).
אלמנטים משולשים
משולשים מורכבים משלוש צלעות הנפגשות בשלושה קודקודים.משולשים מורכבים מכמה אלמנטים, רבים מהם כבר הזכרנו:
- קודקודים. אלו הן הנקודות שמגדירות משולש על ידי חיבור שתיים מהן עם קו ישר. לפיכך, אם יש לנו נקודות A, B ו-C, חיבורן עם קווים AB, BC ו-CA ייתן לנו משולש כתוצאה מכך. כמו כן, הקודקודים נמצאים בצד הנגדי של הזוויות הפנימיות של המצולע.
- צדדים. זהו השם שניתן לכל אחד מהקווים המצטרפים לקודקודים של משולש, התוחמים את הדמות (הפנים מבחוץ).
- זוויות. כל שתי צלעות של משולש יוצרות בקודקוד המשותף שלהן סוג כלשהו של זווית, הנקראת זווית פנימית, מכיוון שהיא פונה אל פנים המצולע. זוויות אלו הן, כמו הצלעות והקודקודים, תמיד שלוש.
סוגי משולשים
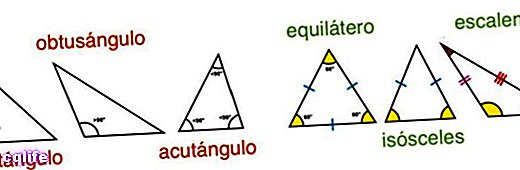
ניתן לסווג משולשים לפי הזוויות שלהם או לפי הצלעות שלהם.
ישנם שני סיווגים עיקריים של משולשים:
- לפי הצדדים שלו. בהתאם ליחס בין שלוש הצלעות השונות שלו, משולש יכול להיות:
- שְׁוֵה צְלָעוֹת. כאשר לכל שלושת הצדדים יש אותו הדבר בדיוק אורך.
- שְׁוֵה שׁוֹקַיִם. כששתיים מהצלעות שלו באותו אורך והשלישית שונה.
- סולם. כאשר לשלושת הצדדים שלו יש אורכים שונים זה מזה.
- לפי הזוויות שלהם. בהתאם לפתיחת הזוויות שלו, אנו יכולים לדבר על משולשים:
- מלבנים. הם מציגים זווית ישרה (90 מעלות) המורכבת משתי צלעות דומות (רגליים) והפוכות לשלישית (hypotenuse).
- זוויות אלכסוניות אלה שאינם מציגים זווית ישרה, וזה בתורו יכול להיות:
- זוויות קהות. כאשר כל אחת מהזוויות הפנימיות שלו קהה (יותר מ-90 מעלות) ושתי האחרות חדות (פחות מ-90 מעלות).
- זוויות חדות. כאשר שלוש הזוויות הפנימיות שלו חדות (פחות מ-90 מעלות).
ניתן לשלב את שני הסיווגים הללו, מה שמאפשר לנו לדבר על משולשים ישרים שוקיים, משולשים חדים בקנה מידה וכו'.
היקף של משולש
היקף משולש מחושב על ידי הוספת צלעותיו.היקף משולש הוא סכום אורכי צלעותיו, ובדרך כלל מסומן באות ע או עם 2 שניות. המשוואה לקביעת היקפו של משולש נתון ABC היא:
p = AB + BC + CA.
לדוגמא: משולש שצלעותיו 5 ס"מ, 5 ס"מ ו-10 ס"מ יהיה בעל היקף של 20 ס"מ.
שטח של משולש
כדי לחשב את שטח המשולש יש צורך לדעת את גובהו.שטחו של משולש (א) הוא החלל הפנימי התחום בשלושת צלעותיו. ניתן לחשב אותו בהכרת הבסיס שלו (ב) וגובהו (h), לפי הנוסחה:
a = (b.h)/ 2.
השטח נמדד ביחידות אורך בריבוע (ס"מ, מ"ר, קמ"ר וכו')
בסיס משולש הוא הצלע שעליה "נשענת" הדמות, בדרך כלל התחתית. במקום זאת, כדי למצוא את גובהו של משולש, עלינו לצייר קו מהקודקוד שממול לבסיס, כלומר, הזווית העליונה. הקו הזה צריך ליצור זווית ישרה עם הבסיס.
כך, למשל, בעל משולש שווה שוקיים עם צלעות: 11 ס"מ, 11 ס"מ ו-7.5 ס"מ, נוכל לחשב את גובהו (7 ס"מ) ולאחר מכן ליישם את הנוסחה: a = (11 ס"מ x 7 ס"מ) / 2, אשר מניבה תוצאה של 38.5 סמ"ר.
דמויות גיאומטריות אחרות
הריבוע, המלבן והעיגול הם הדמויות הגיאומטריות הפשוטות האחרות.דמויות גיאומטריות דו מימדיות אחרות בעלות חשיבות הן:
- הכיכר. מצולעים עם ארבע צלעות שוות לחלוטין, אבות דו מימדיים של הקובייה.
- המלבן. אם ניקח ריבוע ונאריך שתיים מצלעותיו הנגדיות, נקבל דמות המורכבת מארבעה קווים: שניים שווים ושניים שונים (אך שווים זה לזה). זה מלבן.
- המעגל. כולנו מכירים את המעגל, אחת הצורות הפשוטות ביותר של גיאומטריה ואשר מורכב מקו מעוקל רציף שחוזר לנקודת ההתחלה המתווה 360 מעלות של היקף.
